SemanticModels.jl: Not Just Another Modeling Framework

James Fairbanks & Christine Herlihy

JuliaCon2019

• Teaching computers to do science
• Project Repo github.com/jpfairbanks/SemanticModels.jl

Scientific Modeling

• Scientists make models out of math
• Models need to be implemented as code
• When you change the math, you need to change the code!

Modeling Frameworks

Most frameworks are designed before the models are written

Framework	Math	Input Specification	Description
Matlab/Scipy	x = A\b	BLAS + scripting	Sci/Eng math is all BLAS
Mathematica	$p(x)=0$	Symbolic Math Expressions	Computer Algebra Systems
Stan	$ y \sim \mathcal{N}(x \beta + \alpha, \sigma)$	StanML	Bayesian Inference
	$\min_{x\perp C(x)} f(x)$	AMPL based DSL	Optimization Problems
	$y\approx f(x)$	TF.Graph	Deep Learning
SemanticModels.jl	All Computable Domains	Julia Programs	$Models \subset Code$

SemanticModels is a post hoc modeling framework

What is a Modeling Framework?

1. Objects: $X,Y,Z$
2. Models: $f:X\rightarrow Y$, $g: Y\rightarrow Z$
3. Composition: $g\circ f: X\rightarrow Z$
4. Combination: $f\otimes g: X\otimes Y \rightarrow Y\otimes Z$
5. Executability: $\texttt{foo} = eval(f) \implies \texttt{foo(x::X)::Y}$ runs the model

Mathematical Diagrams are pervasive

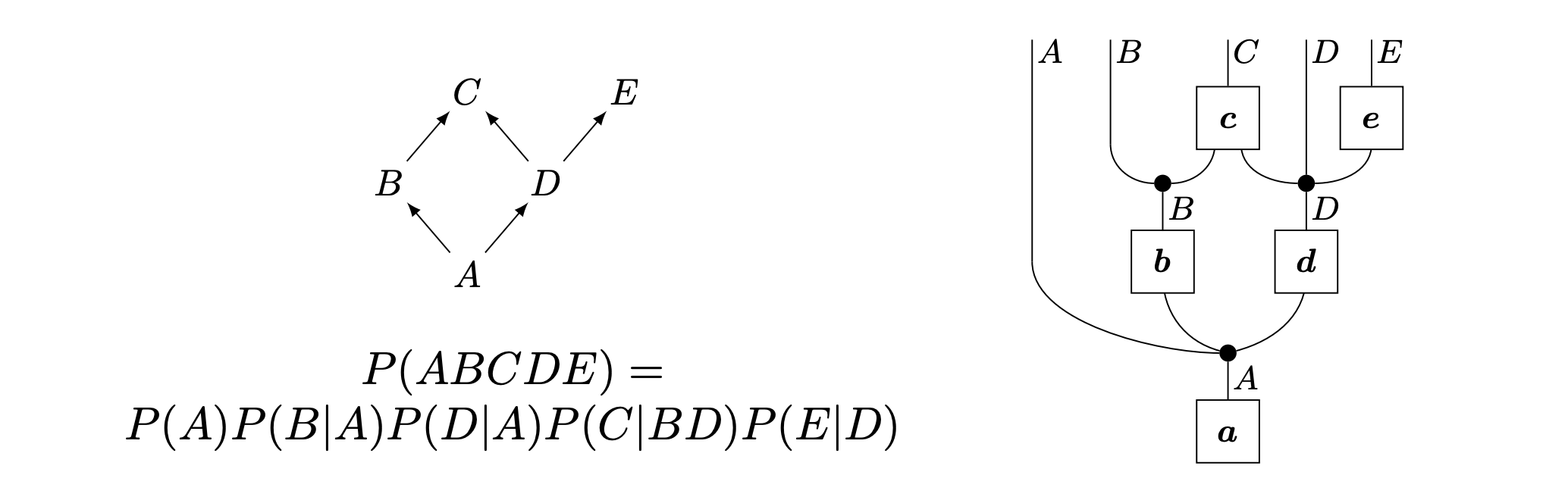Two perspectives on Bayesian Networks (Jacobs, Kissinger, and Zanasi, 2019)

Scientists love diagrams

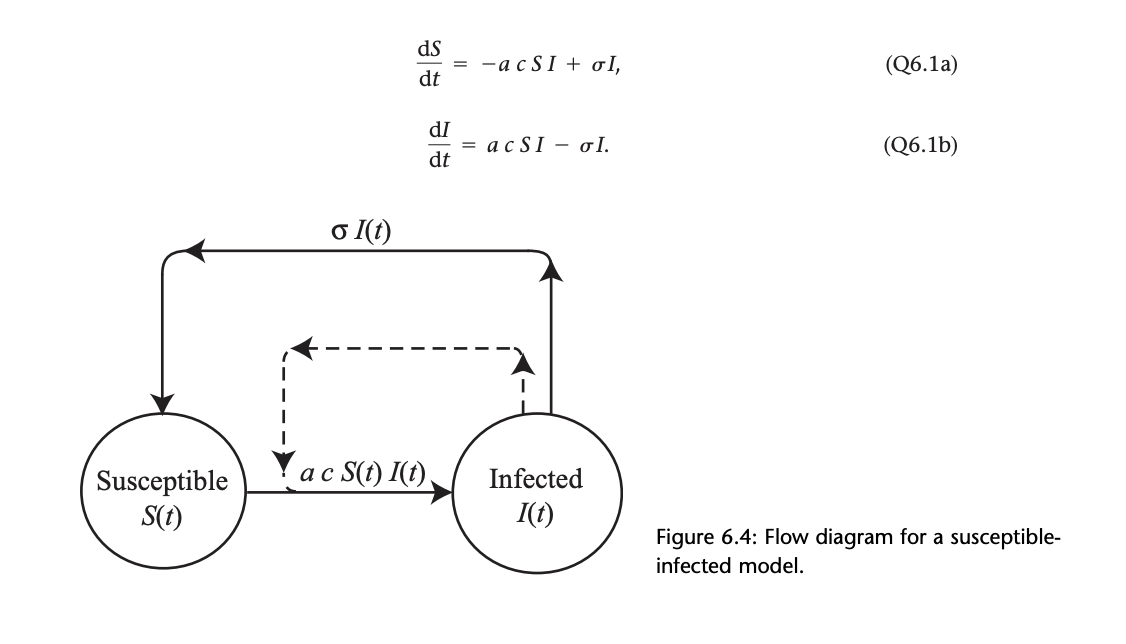The SIS Model (figure from A Biologist's guide to Mathematical Modeling in Ecology and Evolution By Sarah Otto and Troy Day 2007)

SIR model of disease

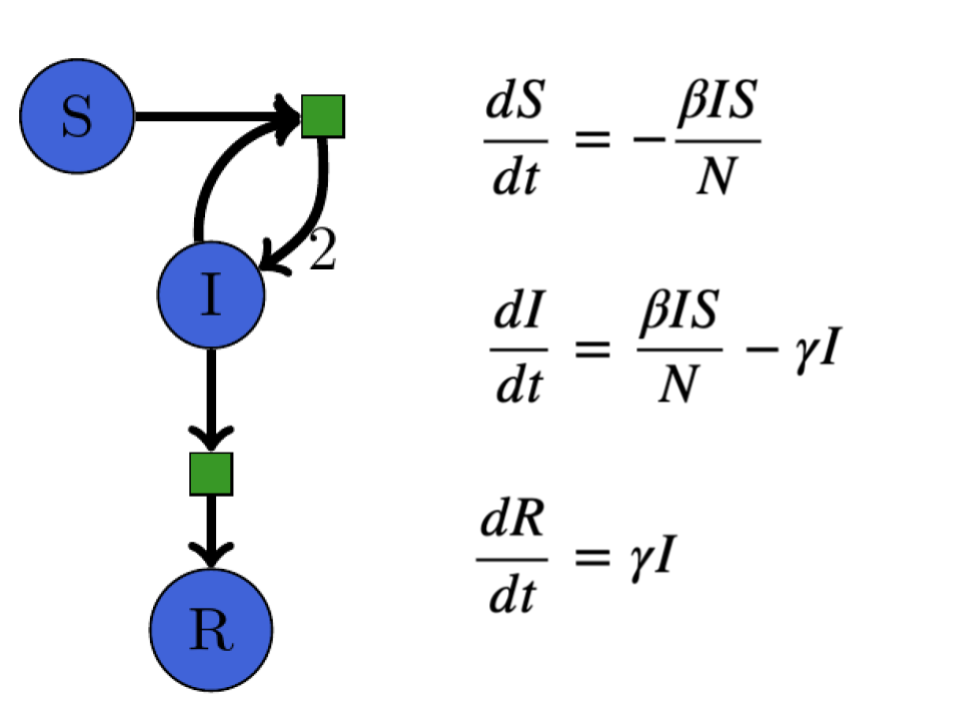The SIR model shown with equivalent Petri net and system of ODEs

SIR predicts real diseases

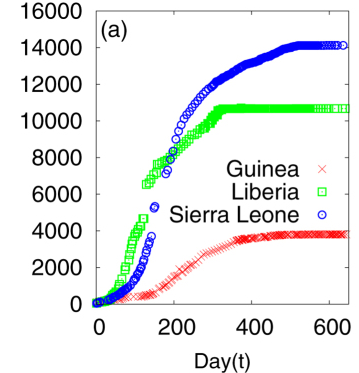Ebola Outbreak Data

• (a) Cumulative number of infected individuals as a function of time (day) for the three countries Guinea, Liberia and Sierra Leone.

• A Khalequea, and P Senb, "An empirical analysis of the Ebola outbreak in West Africa" 2017

ODE Based Implementation

This is a "real world" implementation of SIR modeling in Julia taken from Epirecipes Cookbook (Simon Frost)

module SIRModel
using DifferentialEquations

function sir_ode(du, u, p, t)
    #Infected per-Capita Rate
    β = p[1]
    #Recover per-capita rate
    γ = p[2]
    #Susceptible Individuals
    S = u[1]
    #Infected Individuals
    I = u[2]
    du[1] = -β * S * I
    du[2] = β * S * I - γ * I
    du[3] = γ * I
end

#Param = (Infected Per Capita Rate, Recover Per Capita Rate)
param = [0.1,0.05]
#Initial Params = (Susceptible Individuals, Infected by Infected Individuals)
init = [0.99,0.01,0.0]
tspan = (0.0,200.0)

sir_prob = ODEProblem(sir_ode, init, tspan, param)

sir_sol = solve(sir_prob, saveat = 0.1);

Agent based simulation

""" Agent Models is a hypothetical ABM framework"""
module AgentModels

abstract type AgentModel end
mutable struct StateModel{T} <: AgentModel
    states::Vector{Symbol}
    data::T
    events::Vector{Function}
    rates::Vector{Number}
end

solve(m::StateModel) = return thesolution(m)
end

using AgentModels #hypothetical ABM framework

function main(nsteps)
    function infection(s)
        if s.S > 0 && s.I > 0
            s.S -= 1
            s.I -= 1
            s.I += 2
        end
    end
    function recovery(s)
        if s.I > 0
            s.I -= 1
            s.R += 1
        end
    end
    states = [:S, :I, :R]
    a = zeros(Int, states)
    ρ = 0.5 + randn(Float64)/4 # chance of recovery
    μ = 0.5 # chance of immunity
    T = [infection, recovery]
    prob = StateModel(states, a, T, [ρ, μ])
    soln = solve!(sam, nsteps)
    return soln
end

Model Augmentation as a Lens

We want scientists to program using lenses

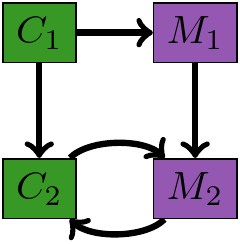Module Augmentation as a Lens

What should the $M_1, M_2$ be?

A Story of an Infectious Disease

A Story of an Infectious Disease

A Story of an Infectious Disease

Wiring Diagrams are a universal syntax

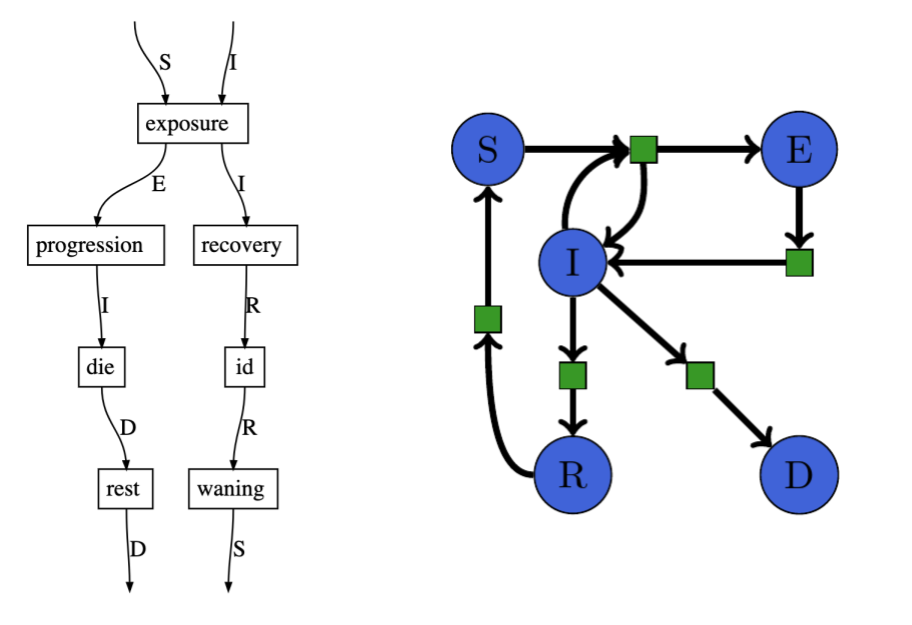Associate all wires with the same label to get a petri net

Petrinet SIR Model

using Petri

function main()
    @variables S, I, R
    N = +(S,I,R)

    Δ = [(S+I, 2I),
         (I, R)]

    m = Petri.Model(Δ)
    p = Petri.Problem(m, SIRState(100, 1, 0), 50)
    soln = Petri.solve(p)
    (p, soln)
end
p, soln = main()

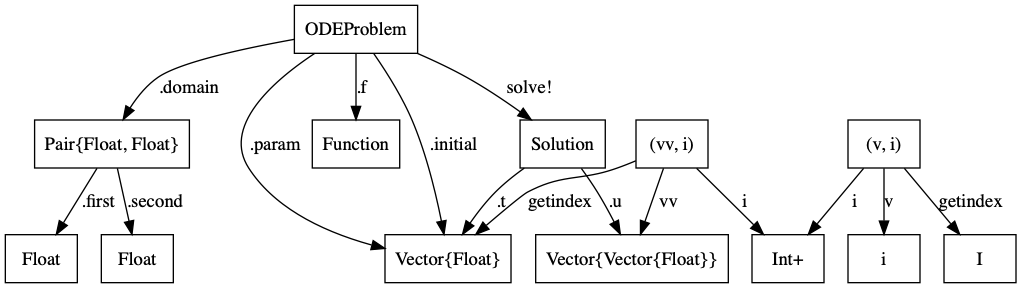
Type Graphs

1. The TypeGraph of a Julia Program tells you a lot about it
2. Computers are good at type checking
3. Can we embed our modeling semantics into the type system?

Structural Model Changes

Modifying models using a Grammar of rewrite rules.

Reasoning by analogy

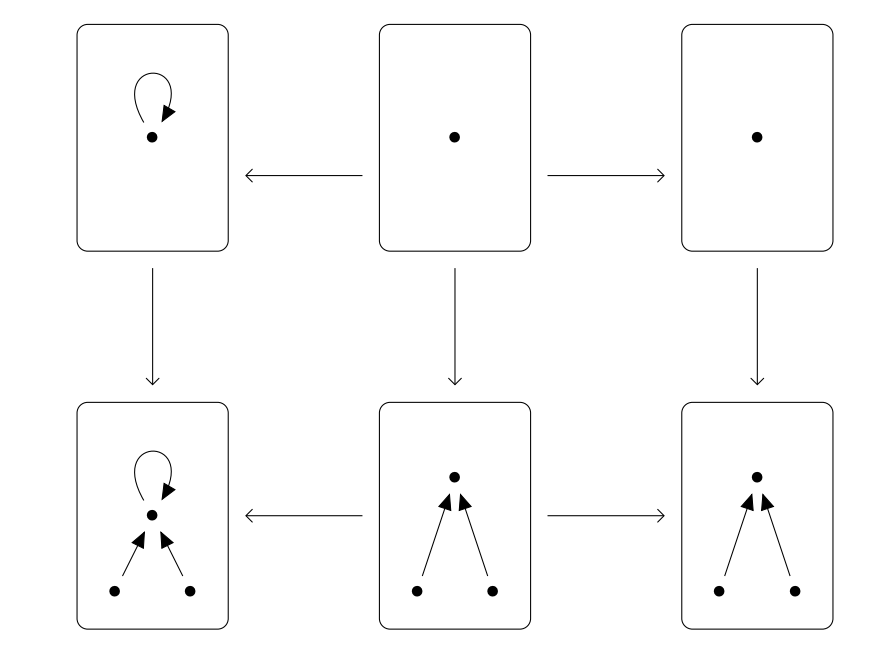Double Push Outs over structured cospans (figure from Cicala, 2019)

Petrinet Model

using Petri

function main()
    @variables S, I, R
    N = +(S,I,R)

    Δ = [(S+I, 2I),
        (I, R),]

    m = Petri.Model(Δ)
    p = Petri.Problem(m, SIRState(100, 1, 0), 50)
    soln = Petri.solve(p)
    (p, soln)
end
p, soln = main()

SIR -> SIRS

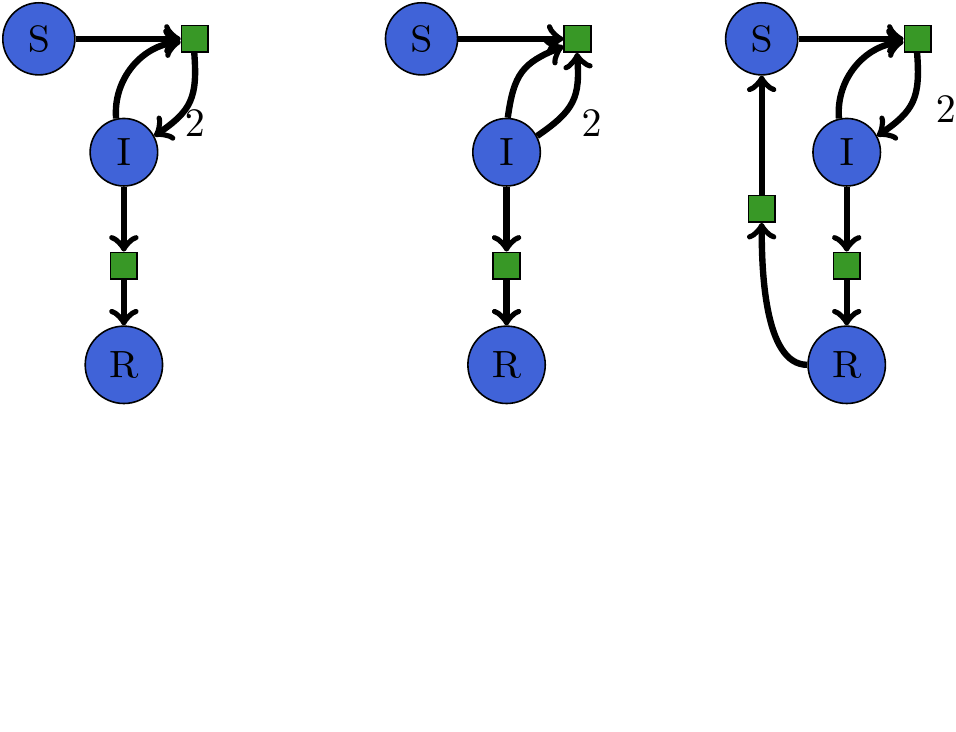
SIRS model as code

using Petri

function main()
    @variables S, I, R
    N = +(S,I,R)

    Δ = [(S+I, 2I),
        (I, R),
        (R, S)]

    m = Petri.Model(Δ)
    p = Petri.Problem(m, SIRState(100, 1, 0), 50)
    soln = Petri.solve(p)
    (p, soln)
end
p, soln = main()

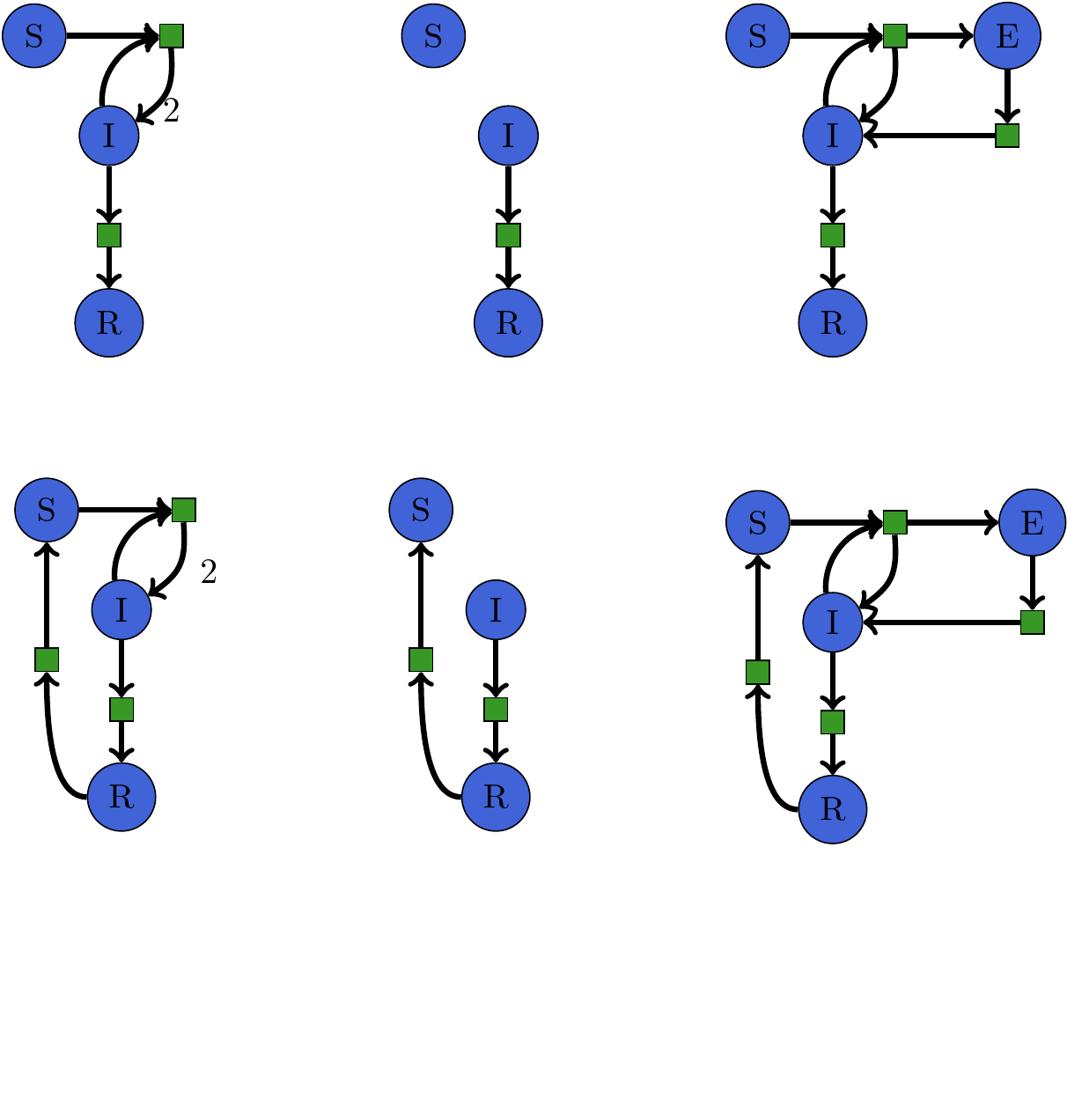
Software Interface for Rewriting Models

states = [S, I, R]

sir = Petri.Model(states,[(I, R), (S+I, 2I)])
ir = Petri.Model(states, [(I, R)])
seir = Petri.Model(states, [(I, R), (S+I, I+E), (E, I)])
rule = Span(sir, ir, seir)

# the root of the bottom of DPO
irs = Petri.Model(states, [(I, R), (R, S)])

sirs, seirs = solve(DPOProblem(rule, irs))

Rewriting Models is a modeling framework

We can recursively define a modeling framework for modeling frameworks!

SEIRS Model as Declarative Code

using Petri

function SEIRSmain()
    @variables S, E, I, R
    N = +(S,E,I,R)

    Δ = [(S+I, I+E),
         (E, I),
         (I, R),
         (R, S) 
    ]

    m = Petri.Model(Δ)
    p = Petri.Problem(m, SEIRState(100, 0, 1, 0), 150)
    soln = Petri.solve(p)
    (p, soln)
end
p, soln = SEIRSmain()

SEIRS Model as Imperative Code

:(##δ#754(state) = begin
          begin
              begin
                  state.I > 0 || return nothing
                  state.I -= 1
              end
              state.R += 1
          end
      end)                                                                                                                                                        
 :(##δ#755(state) = begin
          begin
              begin
                  state.S > 0 || return nothing
                  state.I > 0 || return nothing
                  state.S -= 1
                  state.I -= 1
              end
              begin
                  state.I += 1
                  state.E += 1
              end
          end
      end)
 :(##δ#756(state) = begin
          begin
              begin
                  state.E > 0 || return nothing
                  state.E -= 1
              end
              state.I += 1
          end
      end)                                                                                                                                                        
 :(##δ#757(state) = begin
          begin
              begin
                  state.R > 0 || return nothing
                  state.R -= 1
              end
              state.S += 1
          end
end)

Modeling Frameworks

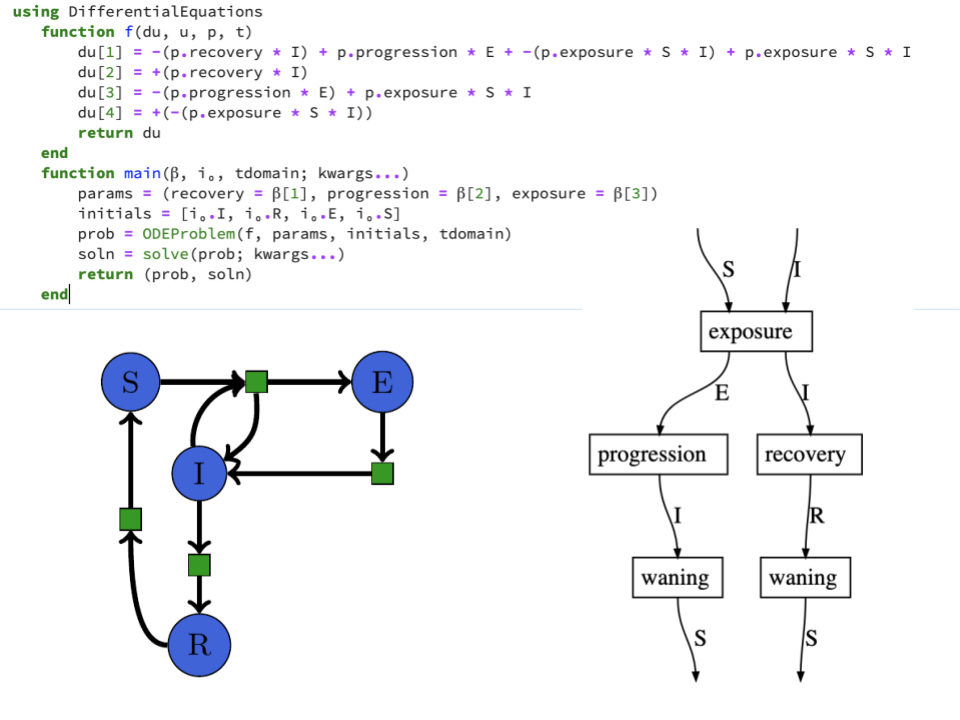
Lenses + Rewriting

Conclusion

1. SemanticModels.jl github.com/jpfairbanks/SemanticModels.jl is a foundational technology for teaching machines to reason about scientific models

2. SemanticModels.jl combines DPO rewriting with Lenses for model augmentation for science!

3. $SemanticModels = Codification \circ Categorification \circ Science $

Open Questions

1. Which scientific modeling frameworks can we represent?
2. How can we compute rewriting for general frameworks?
3. What other modeling activities can we formalize?

Acknowledgements