SemanticModels.jl

• Teaching computers to do science
• Papers are useless, all the information is in code
• Model Augmentation and Synthesis
• Arbitrary models are complex, but transformations are simpler
• Project Repo github.com/jpfairbanks/SemanticModels.jl

What is Modeling?

• Make an initial model $ y \approx \beta x $

• Make a better model $ y \approx \beta x + \gamma y $

• Interpret $\beta, \gamma $ to understand the world

Science as nested optimization

Fitting the data is a regression problem:

$$h^* = \min_{h\in {H}} \ell(h(x), y)$$

Institutional process of discovery is

$$\max_{{H}\in \mathcal{M}} expl(h^*)$$ where $expl$ is the explanatory power of a class of models $H$.

• The explanatory power is some combination of
  • generalization,
  • parsimony,
  • and consistency with the fundamental principles of the field.

Modeling Frameworks

Most frameworks are designed before the models are written

Domain
Algebra
Learning
Optimization
Modeling

SemanticModels is a post hoc modeling framework

SIR model of disease

ODE based simulation

A mathematical model of disease spread

\begin{align} \frac{dS}{dt}&=-\frac{\beta IS}{N}\\\\ \frac{dI}{dt}&=\frac{\beta IS}{N}-\gamma I\\\\ \frac{dR}{dt}&=\gamma I \end{align}

Predictions

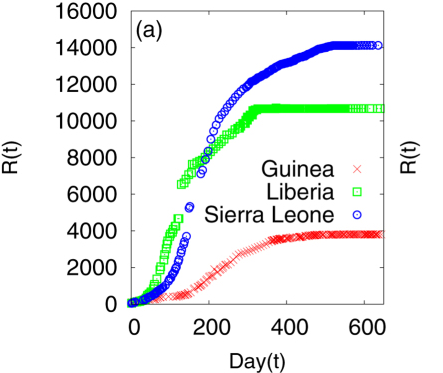
• (a) Cumulative number of infected individuals as a function of time (day) for the three countries Guinea, Liberia and Sierra Leone.
• A Khalequea, and P Senb, "An empirical analysis of the Ebola outbreak in West Africa" 2017

Agent based simulation

abstract type AgentModel end
mutable struct StateModel <: AgentModel
    states
    agents
    transitions
end

#using AgentModels <- hypothetical ABM library

function main(nsteps)
    n = 20
    a = fill(:S, n)
    ρ = 0.5 + randn(Float64)/4 # chance of recovery
    μ = 0.5 # chance of immunity
    T = Dict(
        :S=>(x...)->rand(Float64) < stateload(x[1], :I) ? :I : :S,
        :I=>(x...)->rand(Float64) < ρ ? :I : :R,
        :R=>(x...)->rand(Float64) < μ ? :R : :S,
    )
    sam = StateModel([:S, :I, :R], a, T, zeros(Float64,3))
    newsam = step!(sam, nsteps)
    counts = describe(newsam)
    return newsam, counts
end

main (generic function with 1 method)

Statistical Models

using LsqFit
function f(x, β) 
    return β[1] .* x + β[2]
end

function main()
    X = load_matrix("file_X.csv")
    target = load_vector("file_y.csv")
    a₀ = [1.0]

    fit = curve_fit(f, X, target, a₀)
    return fit
end

main()

Category Theory

CT is the mathematics of structure preserving maps. Every field of math has a notion of homomorphism where two objects in that category have similar structure

1. Sets, Groups, Fields, Rings
2. Graphs
3. Databases

CT is the study of structure in its most general form.

Graphs as Categories

Each graph is a category

• $ G = (V,E) $
• $Ob(G) = V$
• $Hom_G(v,u) = (v\leadsto u) \in E$

The category of graphs

• Graph Homomorphism $f: G\to H$ st $(v\leadsto u) \in G \implies (f(v) \leadsto f(u)) \in H$
• $Ob(Graph)$ is the set of all graphs
• $Hom_{Graph}(G,H)$ is the set of all graph homomorphisms between $G,H$

Models as Categories

Each model is a Category

Category of Models

Semantic Models applies Category Theory

We have built a novel modeling environment that builds and manipulates models in this category theory approach.

Contributions:

1. We take general code as input
2. Highly general and extensible framework
3. Goal: Transformations obey the functor laws.

Example

Show the workflow demo

Functor between models

Define Functor between models

The category of models

While each model can be represented as a category, there is a category of all models.

Functors between models are the morphisms in this category.

Free Monoid of Transformations

Figure of free monoid over a transformation alphabet acting on a model to produce an orbit.

Polynomial Ring acting on Linear Regression

Example

Type Graphs

1. Computers are good at type checking
2. Can we embed our semantics into the type system?

Refining the model

Convert categorical values into singleton types:

The type system "understands" the agents now

Convert categorical values into singleton types:

Conclusion

1. SemanticModels.jl github.com/jpfairbanks/SemanticModels.jl is a foundational technology for teaching machines to reason about scientific models

2. Thinking in terms of transformations on models is easier than thinking of models themselves.

3. A good type system can reason over modeling concepts